Quello su donne e matematica è uno degli stereotipi più duri a morire ed è anche alla base di una presenza “femminile” ancora minoritaria nelle carriere STEM. Qui affrontiamo parte di questo discorso, tra dubbi e cambi di prospettiva – dati alla mano!
Tutti abbiamo sentito in qualche modo dello stereotipo che vorrebbe le donne “meno brave in matematica”, e tutti sappiamo che l’Italia, con il suo 33% circa (fonte: http://data.uis.unesco.org/) di donne nelle carriere cosiddette STEM (“Science, Technology, Engineering, Math”), non sembra affatto sfatare questo mito. Ma quanto è esteso questo stereotipo negli altri Paesi del mondo? Esiste un modo per quantificare la percezione delle proprie capacità? E come cambia la percezione delle proprie abilità matematiche tra maschi e femmine?
NOTA: nell’articolo userò i termini “maschio-femmina” come equivalenti di “uomo-donna”, questo al fine di non generare confusione con l’impostazione dei dati analizzati, in cui non viene operata alcuna distinzione tra sesso biologico e identità di genere, sovrapposti tra loro. Sono consapevole del fatto che usare queste terminologie come sinonimi sia scorretto e anche dell’impianto binario dei dati di partenza. Per questo, a chiusura articolo, propongo una serie di studi in cui la ricerca ha un’impostazione marcata sulle differenze di genere, in quanto si crede che sia quest’ultimo più che il sesso biologico ad essere affetto dallo stereotipo. Nel mio articolo, dunque, dove possibile utilizzerò i termini “uomini e donne”, per evitare una connotazione troppo biologica del discorso; ma i dati di partenza sono riferiti con i termini “male – maschio” e “female – femmina”.
I dati in questione
Essendo un’amante di data analysis, mi sono ritrovata un po’ per caso tra le mani dei dati provenienti da un sondaggio realizzato nel 2012 (il 2012 Gallup World Poll) in 76 Paesi del mondo, per un totale di circa 80,000 individui. Analizzandoli più da vicino, io e il mio ragazzo Andrey (che proprio non ce la fa a non sbirciare dati quando ne ha davanti e adora parlare di statistica e modelli) ci siamo trovati davanti ad alcune peculiarità che non sono assolutamente nuove per le persone del settore, ma che ci è sembrato interessante condividere.
Una delle domande poste nel sondaggio era la seguente:
Quanto la seguente frase ti rappresenta come persona? Io me la cavo bene in matematica.
Per favore indica la risposta su una scala da 0 a 10, dove 0 significa “Non mi descrive per nulla” e 10 “Mi descrive perfettamente”. È possibile utilizzare ogni numero tra 0 e 10 per indicare il proprio posizionamento sulla scala, ad esempio 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10.
La risposta a questa domanda (il numero tra 0 e 10) viene indicata come “abilità (o competenze) matematiche soggettive” (in inglese “subjective math skills”, per i grafici successivi), e rappresenta appunto la percezione che ognuno ha delle proprie abilità matematiche.
Facciamo un piccolo passo indietro…
Perché ci ha interessato proprio la domanda sulle competenze matematiche soggettive? E come si collega con lo stereotipo delle donne e la matematica?
La letteratura scientifica è piena di ricerche che mirano a individuare correlazioni tra stereotipi e performance dei soggetti che subiscono questi stereotipi, da quelli che riguardano l’etnia o la nazionalità di un individuo, al genere o all’età. Ed effettivamente in questi studi si è riscontrata una diminuzione delle performance degli individui quando questi venivano sottoposti a dei test subito dopo essere stati trattati in modo stereotipato, in una sorta di profezia che si auto-avvera.
Tra questi stereotipi c’è sicuramente quello che vuole le donne “meno brave” o “meno portate” per la matematica. Questo stereotipo e le sue conseguenze sono il cuore della questione delle donne nelle carriere scientifiche, o meglio, della mancanza di donne nelle suddette carriere: chi sostiene la teoria “biologica”, riconduce questa minor presenza a delle preferenze innate e differenti tra uomini e donne, che non possono essere curate da “forzature” di sorta quali quote rosa, per esempio. Chi, invece, sostiene la teoria “sociale”, attribuisce queste differenze alla sopracitata correlazione tra performance e stereotipo (sto semplificando molto questo concetto), sostenendo perciò che eliminando gli stereotipi si potrà eliminare questo circolo vizioso e, di conseguenza, aumentare il numero di donne che si avvicinano alla matematica e a carriere scientifiche.
Può risultare che nessuna delle due posizioni sia corretta, perché il modo in cui nostri geni (quindi la parte biologica) si manifestano dipende fortemente dalle circostanze esterne e, viceversa, le circostanze esterne sono in una certa misura determinate dai geni. Questo dibattito, conosciuto come “nature vs. nurture” (in italiano “natura vs. cultura”), va avanti da moltissimo tempo, e ancora non è chiaro quale ruolo abbia un fattore sull’altro. Ma questa è un’altra storia…
Torniamo ai dati
Abbiamo analizzato i dati del sondaggio concentrandoci principalmente su tre variabili: il genere (qui binario, maschio o femmina [vd. sopra]), le abilità matematiche soggettive (su una scala da 1 a 10, come spiegato all’inizio) e il Paese di provenienza del rispondente al sondaggio.
Attenzione: i grafici, pur essendo immagini, non sono da trattare con superficialità, ma vanno “letti” come se fossero un testo scritto. Cercherò di accompagnarvi nella lettura il più possibile, ma concedetevi il tempo di esplorarli, di capirne il significato e le sfumature, come fareste per un testo scritto.
Le differenze “in media”
La prima cosa che abbiamo fatto è stata calcolare la media dei punteggi che gli individui si assegnavano nelle competenze matematiche, separando tra maschi e femmine per ogni Paese. Dopodiché abbiamo sottratto la media calcolata per gli uomini meno la media calcolata per le donne, e il risultato si può osservare nel grafico qui sotto:
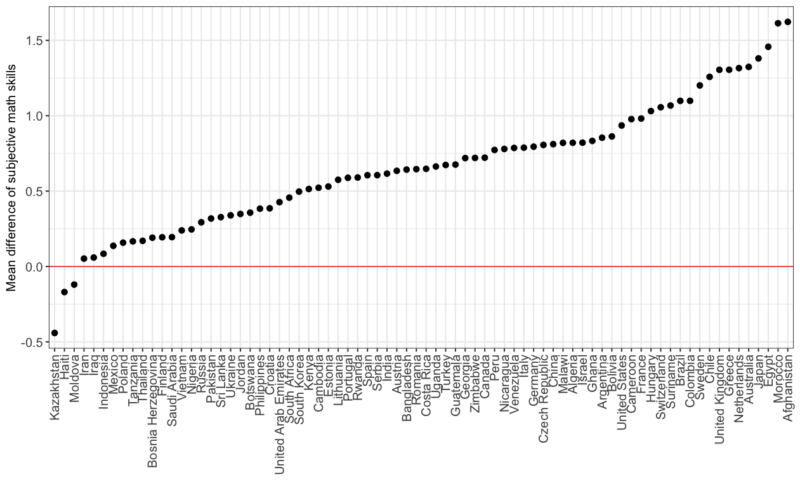
La linea rossa rappresenta lo “0”, ossia il punto in cui non esistono differenze tra la media delle donne e quella degli uomini. Sopra la linea rossa si trovano i Paesi in cui le donne si sono assegnate in media un punteggio inferiore rispetto agli uomini, mentre sotto la linea rossa si trovano i Paesi in cui le donne si sentono più sicure degli uomini delle proprie abilità matematiche. I Paesi sono ordinati per differenze, quindi a sinistra si trovano quelli con differenza negativa e più a destra si trovano quelli con differenze positive sempre maggiori.
Si può notare che praticamente in tutti i Paesi (meno i 3 sotto la linea) le donne tendono a sentirsi meno sicure delle loro abilità matematiche rispetto agli uomini, assegnandosi in media un punteggio inferiore. Ad esempio, guardando il punteggio di Afghanistan e Marocco (gli ultimi due punti in alto a destra), si vede che in media in quei Paesi le donne si sono assegnate circa 1 punto e mezzo di meno rispetto agli uomini. Purtroppo non abbiamo avuto modo di esplorare se esista una relazione tra questi numeri e quanto lo stereotipo delle abilità in matematica delle donne fosse radicato nei Paesi analizzati.
Perché la media non è una buona rappresentante della popolazione
Controllando le distribuzioni delle risposte dei singoli Paesi, possiamo imparare qualcosa di più interessante sulle differenze, che può essere riassunto come la media non è un buon rappresentante della popolazione. Per le persone più abituate a maneggiare dati, questa frase può risultare ovvia, ma è bene sempre tenerlo a mente.
Prendiamo come esempio Italia e Germania, in cui la differenza tra donne e uomini nelle competenze soggettive in matematica sono quasi identiche: tornando al grafico precedente, troviamo questi due Paesi più verso destra, con differenza tra competenze matematiche soggettive tra uomini e donne di circa 0.8 per entrambi.
Se invece della media costruiamo un istogramma delle risposte date, vediamo che queste sono molto diverse tra loro. Nel grafico sotto, la distribuzione in giallo senape rappresenta la distribuzione delle risposte date dalle donne (a sinistra in Italia, a destra in Germania), mentre la distribuzione in grigio è quella delle risposte date dagli uomini. Le righe tracciate rappresentano la media delle risposte (in giallo con linea solida per le donne, in grigio con linea tratteggiata per gli uomini). Le risposte sono proporzionate al numero totale di individui: questo significa, ad esempio, che se troviamo una barra di altezza “0.05”, corrisponderà al 5% delle persone di quel Paese che ha risposto in quella maniera.
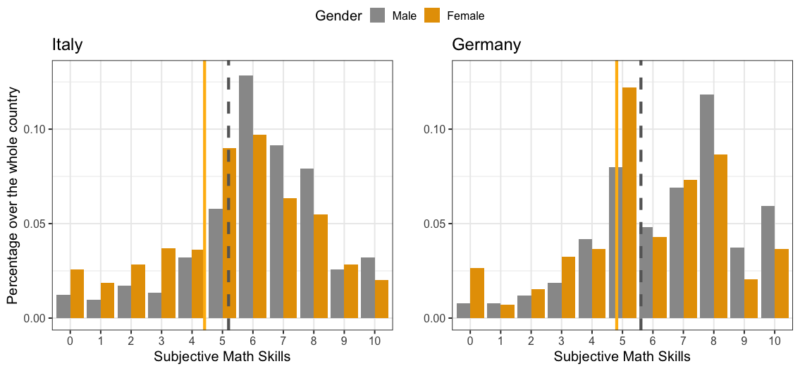
In Italia, la moda, ossia la risposta più frequente di entrambi i generi (maschi e femmine) corrisponde a 6. In Germania, al contrario, la moda delle distribuzioni per i due generi è diversa: i maschi tendono ad assegnarsi un punteggio di 8, mentre le femmine sono molto più moderate e si assegnano maggiormente 5. Guardando lo spazio tra la linea gialla e la linea grigia (quindi di nuovo la differenza delle medie), ci si rende conto che questa differenza è la stessa. Da qui la riflessione sul fatto che quando un risultato viene riportato “in media”, soprattutto quando si riferisce a una scala di valori discreti (ad esempio, da 1 a 10, o con risposte del tipo “Molto d’accordo”, “Neutrale”, “In disaccordo”), non ci sta dando un’informazione completa ed esaustiva.
Un passo in più
Ci siamo domandati come rappresentare in modo più completo le differenze osservate, in modo da perdere meno informazione possibile: abbiamo quindi creato una mappa termica 2D, con i Paesi ordinati sulla scala orizzontale e i valori delle competenze matematiche soggettive collocati invece sulla scala verticale.
Il colore blu rappresenta una differenza negativa, quindi un numero inferiore di donne si è assegnata quel valore di abilità matematiche soggettive rispetto ai maschi, mentre il rosso rappresenta una differenza positiva (un numero maggiore di donne si è assegnata quel valore rispetto ai maschi).
L’ordine dei Paesi è lo stesso di quello visualizzato per la media delle differenze, ma questa volta si può vedere chiaramente l’andamento delle differenze: un colore più intenso indica differenze più marcate, mentre il bianco rappresenta l’assenza di differenze.
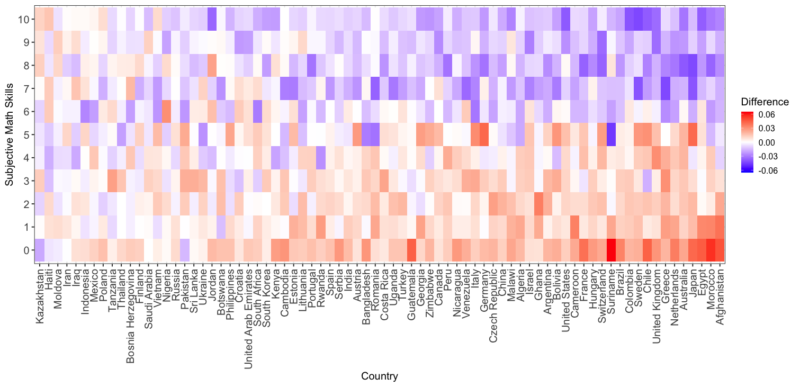
Quello che si nota è che i Paesi così ordinati sembrano sottolineare non solo che andando da sinistra verso destra la media delle differenze aumenta (in direzione positiva), ma anche che nei Paesi più a sinistra, quindi quelli che vedono le donne assegnarsi valori più alti degli uomini, le differenze hanno colori molto meno intensi rispetto alla parte a destra, dove sono i Paesi in cui le donne si assegnano in media dei valori molto più bassi degli uomini.
Questi numeri ci indicano due cose:
• Le differenze massime tra le scelte di uomini e donne nell’assegnarsi questi punteggi sono dell’ordine del percento. Facciamo un esempio con un Paese avente un valore estremo nel grafico, il Suriname. Assumendo che partecipino al sondaggio 1000 persone, ci saranno 70 donne che si assegnano questo valore, contro 10 uomini che se lo assegnano. Questo indica la differenza del 6% della popolazione, indicata dal colore rosso nella casella “0” delle competenze matematiche soggettive.
• Le differenze tendono ad essere più intense nel rosso, concentrandosi nella parte inferiore del grafico. Prendendo sempre l’esempio del Suriname: si vede che, oltre al tassello rosso intenso, abbiamo anche un tassello parecchio blu al centro, corrispondente al “5” delle abilità matematiche soggettive. Semplificando, possiamo pensare che se ci sono 60 donne in più rispetto agli uomini che scelgono di assegnarsi “0”, significa che ci devono essere 60 uomini che scelgono valori più alti. Nel caso del Suriname, questi 60 uomini sembrano aver scelto prevalentemente di assegnarsi “5”.
Tirando le somme
I dati sollevano molte domande ma purtroppo non possono fornire tutte le risposte. Quel che è interessante è la varietà del dataset utilizzato, che si estende in vari Paesi del mondo con grandi differenze socio-culturali, linguistiche e demografiche.
Abbiamo cercato di trovare una correlazione tra la ricchezza dei Paesi e la differenza delle abilità matematiche soggettive tra uomini e donne, utilizzando come indicatore di ricchezza il GDP per capita, ma la correlazione trovata è stata molto debole. Anche controllando il Gender Equality Index (l’indice, costruito da diverse fonti quali le Nazioni Unite e il World Economic Forum, che fornisce una lista ordinata di quanto i Paesi siano o meno a buon punto nell’implementare leggi a favore dell’uguaglianza tra generi) non è stata trovata alcuna correlazione.
Chiaramente questo lavoro non è esaustivo, e il passo successivo sarebbe esplorare ulteriormente quali Paesi hanno differenze maggiori e cercarne le cause in altri indicatori. Sarebbe ad esempio interessante capire se lo stereotipo delle donne meno brave in matematica è correlato alla percentuale di donne nelle carriere scientifiche di quel Paese.
Domande aperte
Ci sono anche altre domande che io e Andrey ci siamo posti senza poter rispondere, come ad esempio:
• Qual è la distribuzione delle competenze matematiche (non soggettive, ma reali) negli individui nei vari Paesi?
• Quanto i Paesi considerati sono orientati verso l’idea che “le donne non sono brave in matematica”?
• La differenza è dovuta all’impatto dello stereotipo “le donne non sono brave in matematica” o è da associare alla minore autostima delle donne?
Un’ultima osservazione: questi dati sono stati interpretati a partire dall’assunto che le donne si ritengono meno brave in matematica per via dello stereotipo che le affligge. La questione però si può porre altrettanto legittimamente al contrario, ossia chiedendosi quanto gli uomini sovrastimano le loro capacità matematiche. Non possiamo sapere quale sia la “domanda corretta” perché ci servirebbero i dati che indicano le reali competenze matematiche di ognuno di questi individui. È interessante però riflettere sul fatto che un cambio del soggetto della domanda possa anche influenzare la prospettiva di analisi dati e di ricerche aggiuntive.
Che altre domande faresti? Sentiti liber* di lasciare un commento!
Altri spunti per la lettura
In italiano, più discorsivi:
• Stereotipi e la percezione degli altri, Universita’ Sapienza di Roma
• Stereotipi e Pregiudizi, Universita’ degli Studi di Messina
• Stereotipi e Pregiudizi, La Psicologia del Sociale, Sapere.it
• Stereotipi di genere e competenze matematiche, Prof. Maria Chiara Passolunghi
In inglese, più scientifici:
• Steele CM, Aronson J. Stereotype threat and the intellectual test performance of African Americans. J Pers Soc Psychol. 1995 Nov;69(5):797-811. doi: 10.1037//0022-3514.69.5.797. PMID: 7473032.
• Keller J, Dauenheimer D. Stereotype threat in the classroom: dejection mediates the disrupting threat effect on women’s math performance. Pers Soc Psychol Bull. 2003 Mar;29(3):371-81. doi: 10.1177/0146167202250218. PMID: 15273014.
• Pennington CR, Heim D, Levy AR, Larkin DT. Twenty Years of Stereotype Threat Research: A Review of Psychological Mediators. PLoS One. 2016 Jan 11;11(1):e0146487. doi: 10.1371/journal.pone.0146487. PMID: 26752551; PMCID: PMC4713435.
• How to Undo Gender Stereotypes in Math—With Math!, Dr. Eugenia Cheng
